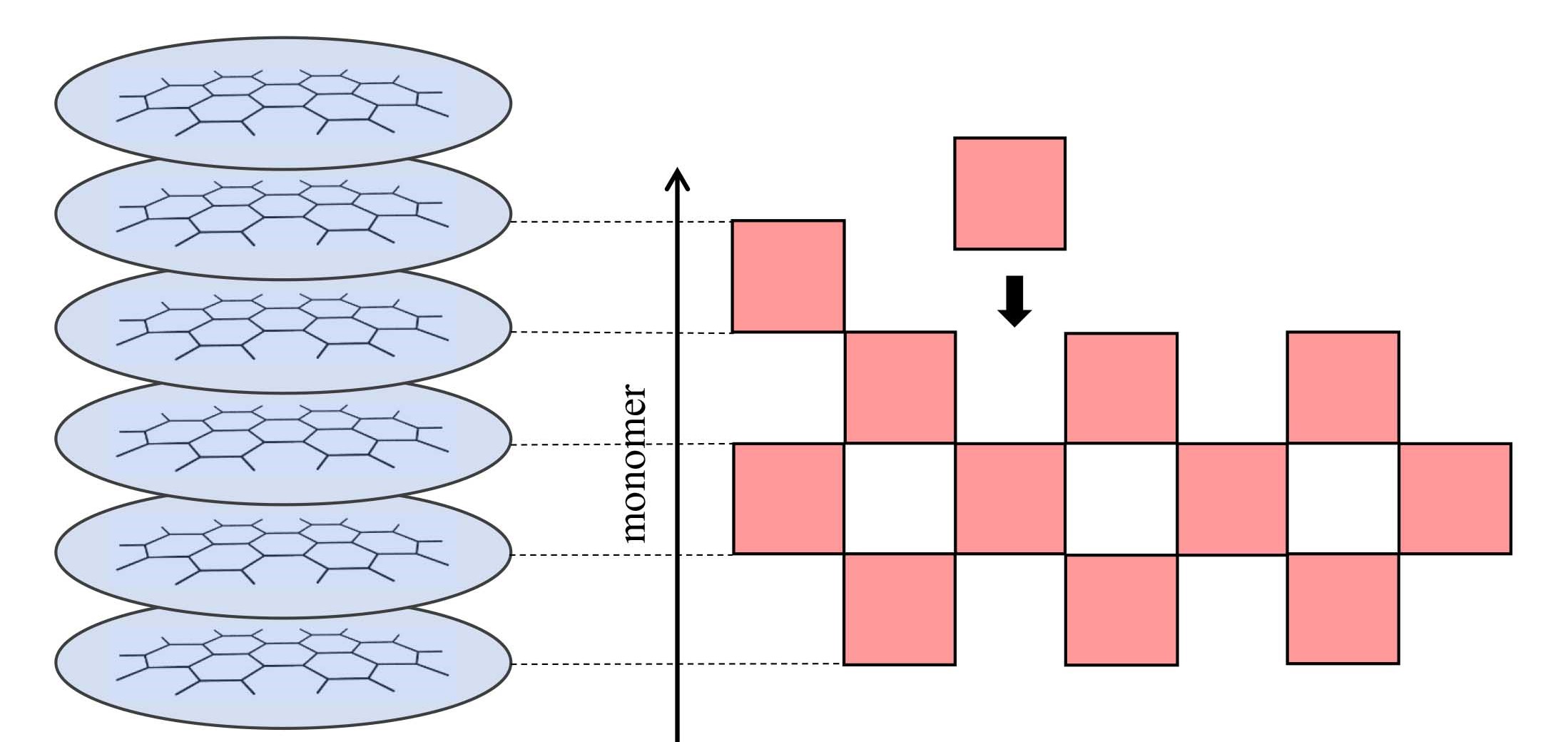
The modular decomposition of the path integral (MPI) is a numerically exact algorithm for calculating dynamical properties of extended systems composed of units with many internal degrees of freedom, which comprise the modules. Each unit can be a molecule comprising discrete spin or electronic states and multiple intramolecular vibrations or phonons. Nearby modules interact via diagonal or nondiagonal couplings. The distinguishing advantage of the MPI algorithm is the combination of (i) linear scaling with system size and (ii) the ability to treat quantum mechanically any number of intramolecular vibrations at finite temperature, without approximation, with practically no increase in computational cost.
The MPI algorithm proceeds by sequentially linking the quantum paths of adjacent units. The linking matrix can be further decomposed into a diagonal matrix and a product of low-dimensional matrices, which can be applied sequentially. This factorization changes the scaling to L log L, where L is the number of quantum paths for each unit, leading to dramatic savings that are analogous to those attained by the fast Fourier transform algorithm.
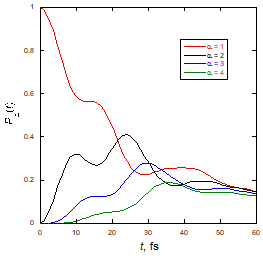
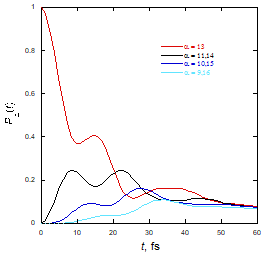
The MPI methodology was used to simulate the exciton-vibration dynamics in a chain of 25 perylene bisimide (PBI) molecules. each of which includes 28 intramolecular normal mode vibrations at 300 K. The left and right panels below show excited state populations of the initially excited and neighboring monomers following excitation of the edge and central molecule.
Related Articles:
- S. Kundu and N. Makri, “Efficient matrix factorization of the modular path integral for extended systems”, Mol. Phys. 2020, DOI: 10.1080/00268976.2020.1797200.
- Kundu and N. Makri, “Modular path integral for finite-temperature dynamics of extended systems with intramolecular vibrations”, J. Chem. Phys. 153, 044124 (2020).
- Kundu and N. Makri, “Modular path integral for discrete systems with non-diagonal couplings”, J. Chem. Phys. 151, 074110 (2019).
- N. Makri, “Modular path integral methodology for real-time quantum dynamics”, J. Chem. Phys. 149, 204108 (2018).
- N. Makri, “Modular path integral: Quantum dynamics via sequential necklace linking”, J. Chem. Phys. 148, 101101 (2018).